If x y z = 0, show that x^3 y^3 z^3 = 3xyz (with Video) Ex 25, 13If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0,x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx)x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proAns 1, 3, 4 15 The relation R on A = {x,y,z} where R = {(x,x),(y,z),(z,y)} Ans 2 16 The relation R on Z where aRb means a ≠ b Ans 2 17 The relation R on Z where aRb means that the units digit of a is equal to the units digit of b Ans 1, 2, 4 18 The relation R on N where aRb means that a has the same number of digits as b Ans factorize x y 3 y z 3 z x 3 Mathematics TopperLearningcom 3z3pm4pp Practice Test MCQs test series for Term 2 Exams ENROLL NOW
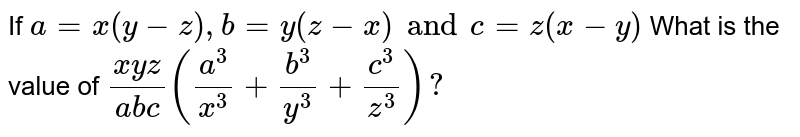
Factorize I A B 3 B C 3 C A 3 Ii X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3
Factorize (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3
Factorize (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3-Factor(x^3y^3z^3 ) Natural Language;Answer (1 of 2) Expression = (xy)(x y) (yz)(y z) (zx)(z x) 2(x)(y)(z) = (xy)(x y z) (yz)(x y z) (zx)(z x) = (xy yz)(x y z) (zx)(z x




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video
Capítulo 1 Factorización 11 Factorizar las siguientes expresiones algebraicas como producto de un binomios y un trinomio 1 4x14y xy y2Sol (8y)(6 xy) 2 −28−4x−4xy 7z xz xyzSol (7xxy)(−4z) 3 18−6x−3xy x2y −3yz xyzSol (−3x)(−6xy yz)4 10x2 x3y 10xz 10yz x2yz xy2zSol (10xy)(x2 xz yz) 5 18−9z −3yz z2 yz2 Use sum of cubes identity to find x^3y^3z^3 = (xyz)(x^2y^2xyzz^2) Use the sum of cubes identity a^3b^3=(ab)(a^2abb^2) with a=xy and b=z as follows x^3y^3z^3 =(xy)^3z^3 =((xy)z)((xy)^2(xy)zz^2) =(xyz)(x^2y^2xyzz^2) Without finding cubes, factorise 1(xy)3 (yz)3 (zx)3 2(x2y)3 (2y3z)3 (3zx)3 Get the answers you need, now!
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicSOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sides So it factors as $(xyz)(Ax^2 Ay^2 Az^2 Bxy Byz Bxz)$ Then let $x = 0$ and we get $(yz)(\text{something}) = y^3 z^3$ This is a wellknown factorization, and the students can easily tell you what 'something' is Then we quickly get $A = 1$, $B = 1$
To factorise z 3 1 into a linear and quadratic factor, it is best to try the factor theorem first We set the equation to zero z 3 1=0We need to find a value of z such that the above is true By inspection we can see that if z=1 then the above is true because (1) 3 1=0 since (1) 3 =1Therefore, (z1) is a factor The other factor is quadraticHere, the exponent of the second term, ie, x–1 is –1, which is not a whole number So, this algebraic expression is not a polynomial Again, x 3 can be written as 1 2 x 3 Here the exponent of x is 1 2, which is Supritha, added an answer, on 3/10/15 Supritha answered this It is form of (a)^ 3 (b)^ 3 (c)^3 =3abc where abc=0 a=xy , b=yz , c=zx abc= 0 = (xy) (yz) (zx)=0 = xyyzzx=0 = 0 =0 (a)^ 3 (b)^ 3 (c)^=3abc
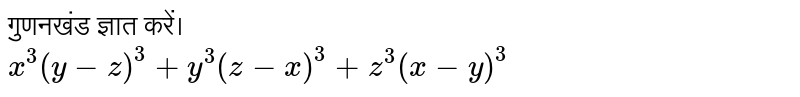



Factorize X Y 3 Y Z 3 Z X 3




Factorize X Y 3 Y Z 3 Z X 3 Youtube
You can use an identity like a^3b^3=(ab)(a^2abb^2) for 2 of the cubes, and hope that it might end up having something in common with the third cube Let's see (2xyz) ^3 (2yzx) ^3= (2xyz2yzx)P(x,y,z)=(xy2zLaintegraldesuperficie Es una elipse en el plano z = y 1 Su proyección sobre el plano XY es la curva ° de ecuación x2 (y ¡1)22 = 1 (una elipse, también) Sea S la superficiedelplano z = y 1 limitadaporC;sepuedeparametrizarcomo r(x;y) = (x;y;y 1);Using the above identity taking a=x−y, b=y−z and c=z−x, we have abc=x−y y−zz−x=0 then the equation (x−y) 3(y−z) 3(z−x) 3 can be factorised as follows (x−y) 3(y−z) 3(z−x)




Dulytraction Nif 3 X Y 5 Y Z 7 Z X From N 5 X Y 2 Y Z 2 Z X 10 X Y Z




X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3 Youtube
= (x y)(x – y)(x 4 x 2 y 2 y 4), by (1) (b) x 6 – y 6 = (x 3) 2 – (y 3) 2 = (x 3 y 3)(x 3 – y 3), by (1) = (x y)(x 2 – xy y 2)(x y)(x 2 xy y 2), by (2) and (3) Which of the above factorization is correct?Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16 factorise the following a) (xy) 3 (yz) 3 (zx) 3 b) 25x 2 16y 2 4z 2 40xy16yz zx c) 1 64x 3 d) 2root2a 3 8b 3 27c 3 18root2 abc e) 842r
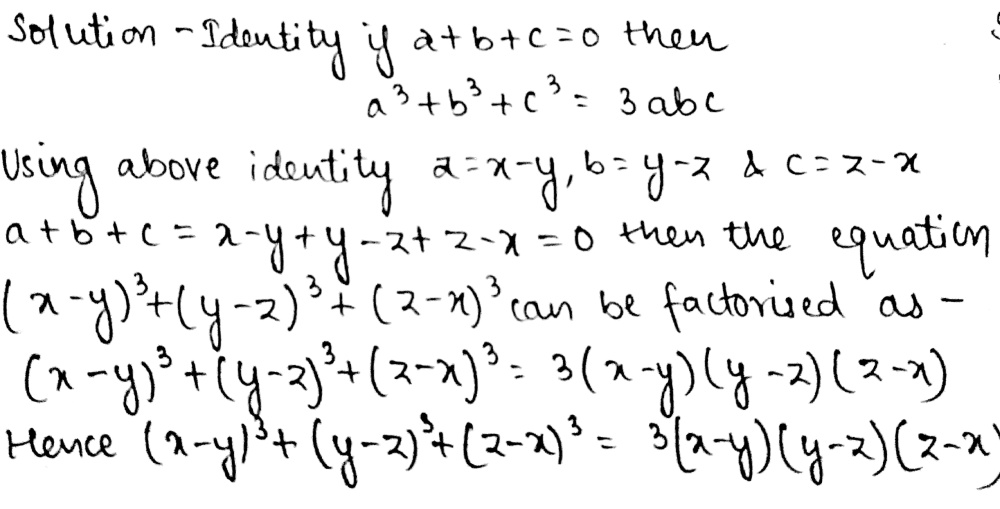



5 Factorise Tex X Y 3 Y Z 3 Z X 3 Tex Snapsolve



How To Factorize 3 3x 3 Y 3 Quora
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Factorize (i)`(ab)^3(bc)^3(ca)^3 `(ii) `x^3(yz)^3y^3(zx)^3z^3(xy)^3` Now we need to factor (x^4 2x^3(yz) 2x^2(yz)^2 x(yz)^3 yz(y^2z^2yz) 1 This has a factor x y and also x z so we have a factor (x^2(yz)x yz) so let other factor be (x^2axc) (x^2(yz)x yz) (x^2axc) = x^4 x^3(ayz) x^2(ca(yz) yz) x(ayzc(yz)) cyz) 2 Comparing coefficients from 1 and 2 From x^3 a= yz,Z = x2y3 2x4y ∂z/∂x =2xy3 2 ∂z/∂y =3x2y2 4 • REMEMBER When you are taking a partial derivative you treat the other variables However, we can treat dy/dx as a fraction and factor out the dx dy = f0(x)dx where dy and dx are called differentialsIfdy/dx can be interpreted as




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1 Youtube
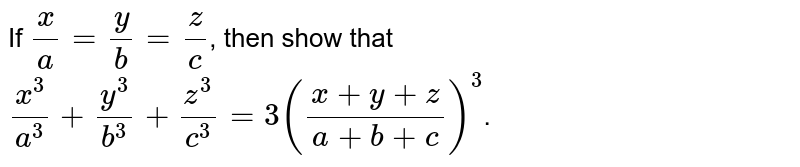



Factorize I A B 3 B C 3 C A 3 Ii X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3
Example 1 Factorize x 2 y 2 y 2 Solution Completely factorize x 2 y 2 y 2, ie write the greatest common factor of x 2 y 2 and y 2 as the common factor y 2 is the highest common factor To find the other factor, divide each term by the HCF and add the quotients (x 2 y 2)/y 2 = x 2 and y 2 /y 2 = 1 Sum of the quotients is x 2 1, which is the other factorTherefore,If f(z) = u(x;y)iv(x;y), where z = xiy, explain why f(z) is analytic and write a formula forf0(z) in terms of the derivatives of uand v Since the derivatives ux, uy, vx and vy are everywhere de ned and continuous and since the CauchyRiemann equations hold everywhere, by our basic theorem on di erentiability, we know that f(z) is di erAlgebra Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In




Find The Value Of X Y Y Z Z X Brainly In
Factoring » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12; Using properties of determinants, prove that (x,y,z)(x^2,y^2,z^2)(x^3,y^3,z^3) = xyz(xy)(yz)(zx)Of course, (b) is the complete factorization, (a) is not Comparing the results in (a) and (b), we can get x 4 x
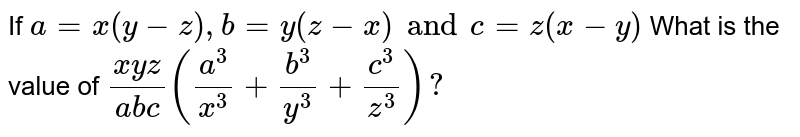



Factorize I A B 3 B C 3 C A 3 Ii X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube
Rewrite x3y3 x 3 y 3 as (xy)3 ( x y) 3 Since both terms are perfect cubes, factor using the sum of cubes formula, a3 b3 = (ab)(a2 −abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = xy a = x y and b = z b = z Simplify Tap for more steps Apply the product rule to x y x y Find the value of k,if y3 is a factor of 3y(to the power square) ky 6 asked in Class IX Maths by muskan15 Expert ( 380k points) polynomialsSubtract 3 x from both sides 2y2z=33x 2 y − 2 z = 3 − 3 x Add 2z to both sides Add 2 z to both sides 2y=33x2z 2 y = 3 − 3 x 2 z The equation is
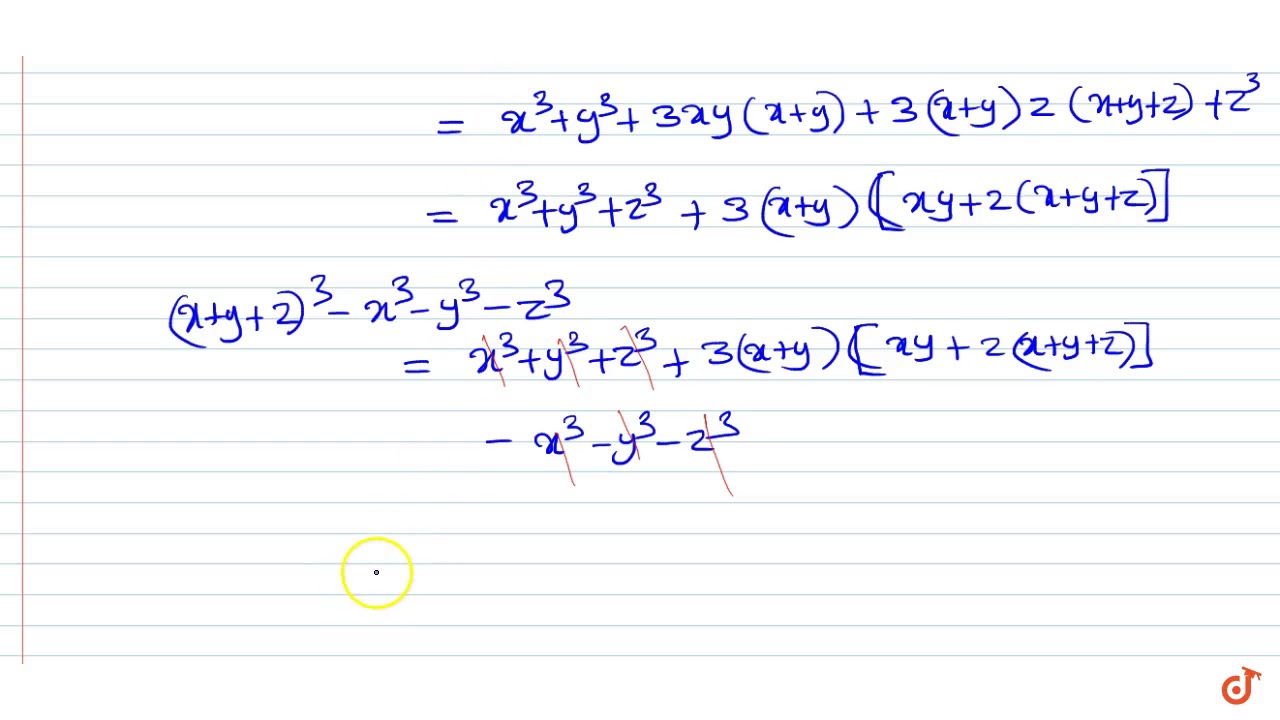



Factorise The Expression X Y Z 3 X 3 Y 3 Z 3 Into Linear Factors Youtube



Q 10 Show That The Expression X 2 Yz 3 Y 2 Zx 3 Z 2 Xy 3 3 X 2 Yz Y 2 Zx Z 2 Xy Is A Perfect Square And Find Its Square Roots
Factor x 3 y 3 z 3 − 3 x y z x^3 y^3 z^3 3xyz x 3 y 3 z 3 − 3 x y z The above polynomial is a symmetric polynomial because you can switch any two variables and still get the same polynomial(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzNon –Homogeneous Linear Equations Let us consider the partial differential equation f (D,D') z = F (x,y) (1) If f (D,D') is not homogeneous, then (1) is a non–homogeneous linear partial differential equation Here also, the complete solution = CF PI The methods for finding the Particular Integrals are the same as those for




Phan Tich đa Thức Thanh Nhan Tử X Y 3 Y Z 3 Z X 3 Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải Bai Tập Toan Học Lớp 8 Lazi Vn Cộng




X Y Z 3 Y Z X 3 Z X Y 3 X Y Z 3 24xyz Mathematics Stack Exchange
Factorization is the decomposition of an expression into a product of its factors The following are common factorizations For any positive integer Brilliant Home Courses Today Sign up x^3 y^3 z^3 3 xyz = (xyz) (x^2y^2z^2xyyzzx) x 3 y 3 z 3 This is the Solution of Question From RD SHARMA book of CLASS 9 CHAPTER POLYNOMIALS This Question is also available in R S AGGARWAL book of CLASS 9 You can FSuppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1)where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uv Substituting into equation (1) gives y^3 y = 2v(3u^2 v^2 1)Since v divides the righthand side, it would be nice if it alsodivides the lefthand side,




Factorize X Y 3 Y Z 3 Z X 3 Youtube




Factorisation Of X Y Y Z Z X Brainly In
Factor calculator is an online tool which allows you to calculate factor expressions online Factoring calculator can be used effectively for learning and practice For an example, if we need to find the factor of 6, its factors would be 1, 2, 3 and 6Answer by You can put this solution on YOUR website!(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy




Factorise 2x Y Z 2y Z X 2z X Y Brainly In




Factorise Xy 3 Yz 3 Zx 3 Maths Polynomials Meritnation Com
Answer (1 of 3) Can you factorize (2xyz) ^3 (2yzx) ^3 (2zxy)^3? 96y 3 z 4 d 4 = 2 × 2 × 2 × 2 × 2 × 3 × y × y × z × z × z × z × d × d × d × d Question 15 The common factor of 36p 2 q 3 x 4 , 48pq 3 x 2 and 54p 3 q 3 x 4 isPago único $1999 USD por 3 meses Weekly Subscription $249 USD por semana hasta cancelar Suscripción mensual $799 USD por cada mes hasta cancelar Promoción de vacaciones Suscripción anual $1999 USD por 12 meses (40% de descuento)



X2 Y2 3 Y2 Z2 3 Z2 X2 3 2 23 2 23 53 3 X Y Scholr



If Xy 2 A 3 Yz 2 B 3 And Zx 2 C 3 Then What Does Z 3 Equal To Quora
Consider x 3 y 3 − z 3 3 x y z as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {3} and m divides the constant factor y^ {3}z^ {3} One such factor is xyz Factor the polynomial by dividing it by this factor (y^2 6y 9)(y 3) So can you please explain (with detailed solution) how this is apparently incorrect (and yes i know it can be expanded further i deliberately didn't expand it further) and yes i know what "simplifying" is, i didnt simplify because i hadn't yet fully expanded it and that would take it out of the ()() form, which isNow, consider algebraic expressions such as x 3 2 1, x y y 3 and x Do you know that you can write x 1 x = x x–1?




Factorize 2x Y Z 3 2y Z X 3 2z X Y 3 Maths Polynomials Meritnation Com




Chapter 3 More About Factorization Ppt Download
Click here👆to get an answer to your question ️ Without finding the cubes, factorise (x 2y)^3 (2y 3z)^3 (3z x)^3(x;y) 2 D = (x;y) 2 R2 x2 (y ¡1)22 • 1 ¾ 3 Calculelaintegral Z SGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




X2 Y2 Y2 Z2 Z2 X2 X Y 3 Y Z 3 Z X 3 Maths Polynomials Meritnation Com




Factorise 2x Y Z 3 2y Z X 3 2z X Y 3 Brainly In
Transcript Ex 42, 9 By using properties of determinants, show that 8 (x&x2&yz@y&y2&zx@z&z2&xy) = (x – y) (y – z) (z – x) (xy yz zx) Solving LHS 8 (𝑥&𝑥^2&𝑦𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Applying R1→ R1 – R2 = 8 (𝑥−𝑦&𝑥^2−𝑦^2&𝑦𝑧−𝑥𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2Factorise (X Y)3 8x3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Factorise (X Y)3 8x3 Mathematics AdvertisementDoing polynomial division you will find x 3 z − x 3 y − y 3 z y z 3 x y 3 − x z 3 = ( x − y) ( x 2 z x y z y 2 z − x 2 y − x y 2 − z 3) Now you can repeat this process on the quantity x 2 z x y z y 2 z − x 2 y − x y 2 − z 3 and factor out another zero, proceeding until




Factorising Cyclic Expression X 2 Y Z Y 2 Z X Z 2 X Y Youtube




Without Finding The Cubes Factorise X Y 3 Y Z 3 Z X 3 Maths Polynomials Meritnation Com
Xyplane, the x and ycoordinates stay the same, but the zcoordinate becomes zero The formula for the transformation is then T x y z = x y 0 ⇀u x T ⇀u y z Let's now look at the above example in a different way Note that the xyplane is a 2dimensional subspace of R3 that corresponds (exactly!) with R2 We can therefore look at the



How To Factorise X 3 3x 2 4 Quora
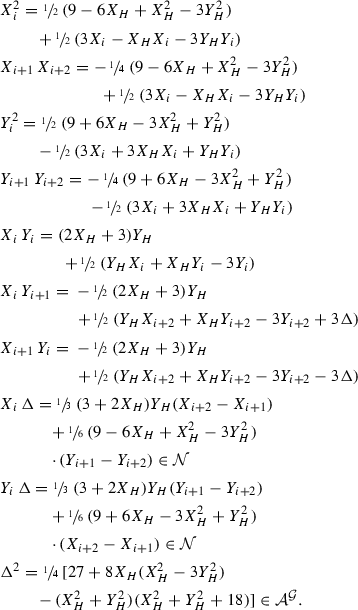



On The Discriminant Of Grunert S System Of Algebraic Equations And Related Topics Springerlink
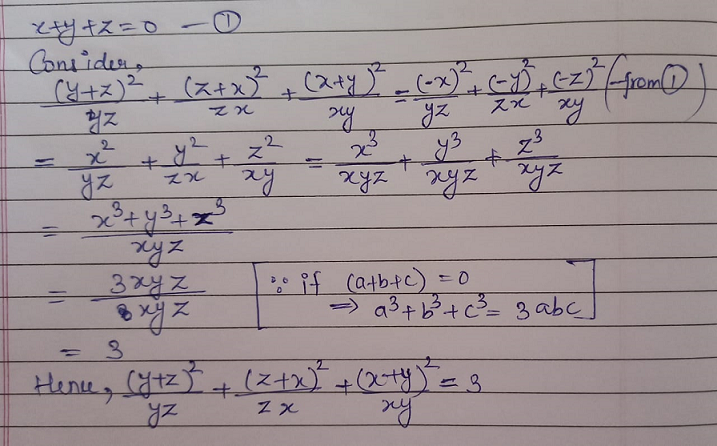



How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



How Can Math X 4 Xz 3 Xy 3 Y 4 Yz 3 X 3y 3xy 2z 3x 2yz Math Be Factored Quora



How To Factor X 2 Xy 2y 2 Yz Zx 4x Y Z 3 Quora



How To Factorise Math Yz 2 Xz 2 Y 2z X 2y X 2z Xy 2 2xyz Math Quora




Factorise 5 X Square 3 Y Square Z Square Minus 2 Root 15 X Y 2 Root 3 Y Square Minus 2 Root 5 Zx Brainly In




Simplify X Y 3 Y Z 3 Z X 3 Maths Polynomials Meritnation Com
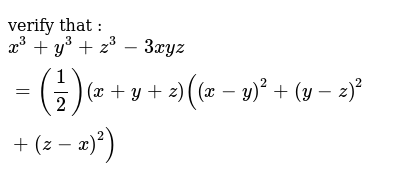



Jossaesipmfbf 人気ダウンロード Simplify X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3
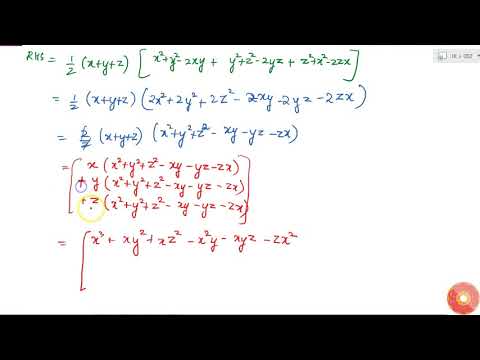



Verify That X 3 Y 3 Z 3 3x Y Z 1




Y Zx




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz Youtube
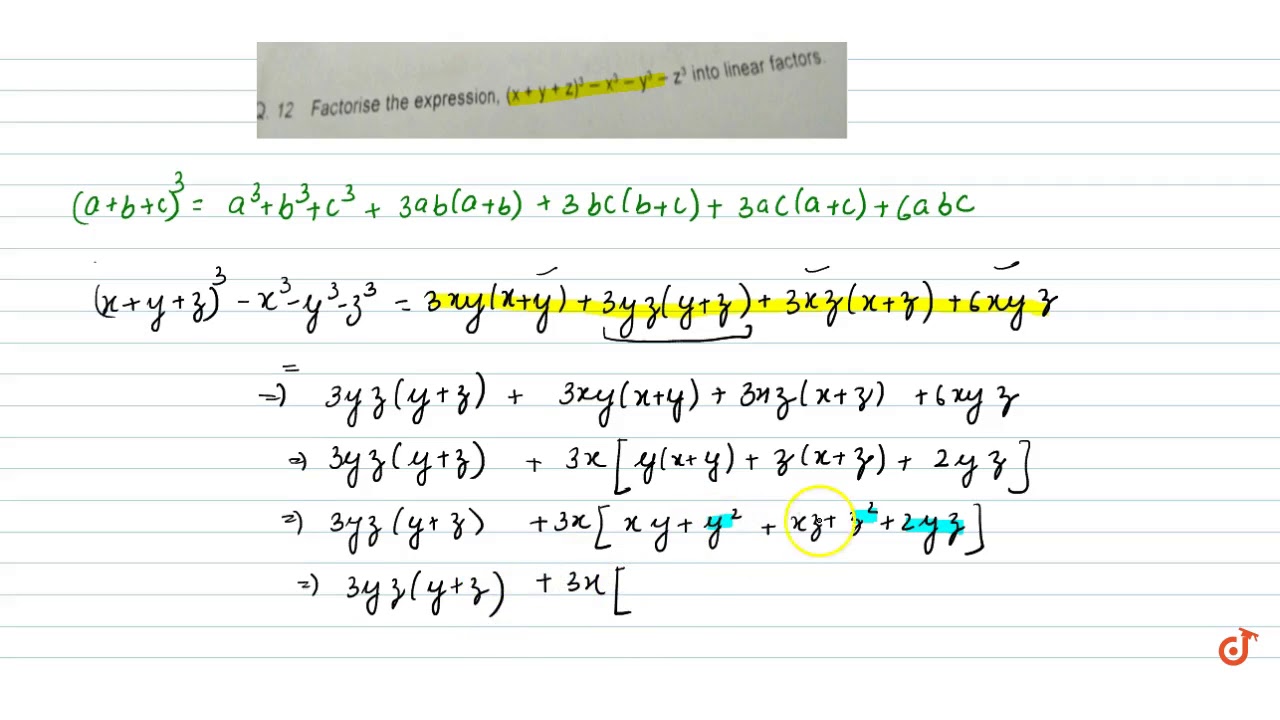



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube




Factorize X3 Y3 Z3 3xyz X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Evaluate Please X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Divided By X Y 3 Y Z 3 Z X 3 Brainly In




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube
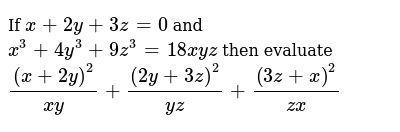



If X 2y 3z 0 And X 3 4y 3 9z 3 18xyz Then Evaluate X 2y 2 Xy 2y 3z 2 Yz 3z X 2 Zx




If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3 Youtube




Factorise 2x Y Z 3 2y Z X 3 2z X Y 3 Brainly In




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55




Find The Directional Derivative Of The Function At The Given Poin




Factorise X Y 3 Y Z 3 Z X 3 Brainly In




Factorize X Y 3 Y Z 3 Z X 3 Youtube




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




Factorise I X Y 3 Y Z 3 Z X 3 Ii X 2y 3 2y 4z 3 4z X 3 Iv 3sqrt 2 A 5sqrt 3 B 3 5sqrt 3 B 7sqrt 5 C 3 7sqrt 5 C 3sqrt 2 A 3



How Can We Factorize X 3 X 2 1 0 Quora




Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Is Equal To A 0 B 1 9 C 1 3 D 1




Chapter 3 More About Factorization Ppt Download



If X Y Z 0 Then X 2 2x 2 Yz Y 2 2y 2 Zx Z 2 2z 2 Xy Sarthaks Econnect Largest Online Education Community




How To Factorize X Y Y Z Z X Quora




Jossaesipmfbf 人気ダウンロード Simplify X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3




Simplify X Y 3 Y Z 3 Z X 3 Brainly In




Factorize X Y 3 Y Z 3 Z X 3




Example 49 Factorise X Y 3 Y Z 3 Z X 3 Solution I Let R U Au H Snapsolve




Factorise The Following A 64 A 3 27 B 3 144 A 2 B 108 A B 2 B X Y 3 Y Z 3 Z X 3



The Value Of X Y 3 Y Z 3 Z X 3 X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Is Sarthaks Econnect Largest Online Education Community




Factorization Of Cyclic And Symmetric Polynomials



How To Solve The Following System Of Equations 3x 2y 2z 2 2x Y Z 2 X 3y Z 0 Quora




Ex 14 1 2 Ix Factorise X 2 Y Z X Y 2z X Y Z 2 Class 8




Factorise X Y 3 Y Z 3 Z X 3 Brainly In




100以上 ƒz ƒx ƒcƒ ƒxƒg 1731




Chapter 3 More About Factorization Ppt Download




Jossaesipmfbf 人気ダウンロード Simplify X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3



What Is The Procedure To Factorise 8a 6 5a 3 1 Quora




Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5



If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Mathematics




Chapter 3 More About Factorization Basic Knowledge Factors




Factorize 8 X Y 3 27 X Y 3 Youtube




Using Factor Theorem Show That X Y Y Z And Z X Are Factors Of X Y Z 3 X3 Y3 Z3 Brainly In




Prove That X Y Y Z Z X 3 X Y Y Z Z Y 2 X Y Z 3xyz Brainly In



12 Of It Is 1080 Snapsolve
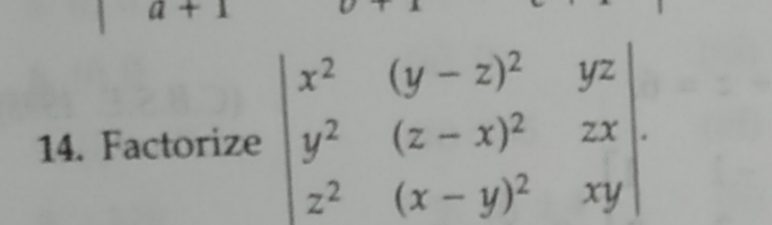



Solved Zx X Y 3 2 Yz 14 Factorize Y Z X X Y 2 Chegg Com




Some Strong Sufficient Conditions For Cyclic Homogeneous Polynomial Inequalities Of Degree Four In Nonnegative Variables Pdf Free Download




The Value Of X Y 3 Y Z 3 Z X 3 9 X Y Y Z Z X Brainly In
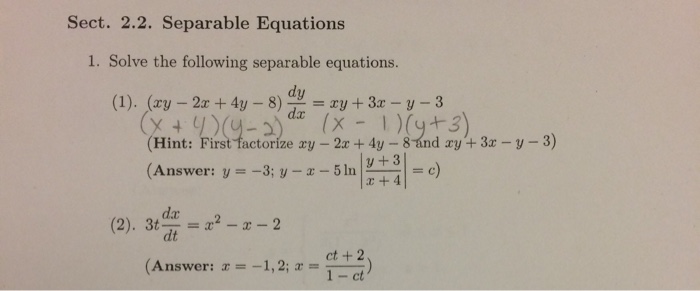



Solved Sect 2 2 Separable Equations 1 Solve The Following Chegg Com




Factorize 2x Y Z 3 2y Z X 3 2z X Y 3 Brainly In



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



2




Factorise 2x Y Z 2y Z X 2z X Y Brainly In




How To Factorize X Y Y Z Z X Quora



Factoring By Grouping Algebra Socratic
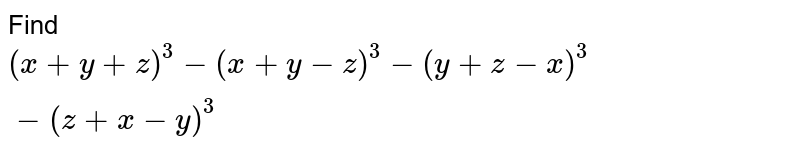



Expansion Of X Y 3 Y Z 3 Z X 3 Is What




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




11 And 12 11 Without Actually Calculating The Cub 12 3 7 3 5 3 12 Without Actually Calculating The Cube Maths Polynomials Meritnation Com




Factorize I A B 3 B C 3 C A 3 Ii X 3 Y Z 3 Y 3 Z X 3 Z 3 X Y 3 Youtube




Using The Identity And Proof X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx




Jossaesipmfbf 人気ダウンロード Simplify X 3 Y 3 3 Y 3 Z 3 3 Z 3 X 3 3 X Y 3 Y Z 3 Z X 3




Factorization Of Cyclic And Symmetric Polynomials



0 件のコメント:
コメントを投稿